Tuas (Pengungkit): Rumus, Keuntungan Mekanis, Contoh Soal
Table of Contents
Tuas atau pengungkit adalah adalah pesawat sederhana yang terdiri atas sebuah batangan kokoh yang dapat berputar mengelilingi sebuah titik.

Apa kabar adik-adik? Semoga kalian selalu dalam keadaan sehat. Materi fisika kita kali ini akan membahas tentang pesawat sederhana tuas atau pengungkit. Materi ini sering dipelajari oleh siswa SD, SMP kelas 8, dan SMA kelas 10.
Sebelumnya, kita telah menuntaskan materi pesawat sederhana lainnya, yaitu bidang miring. Udah paham kan materinya? Nah, bagi yang belum paham, kalian bisa mempelajarinya di sini: Bidang Miring.
Sebagaimana yang telah dijelaskan, pesawat sederhana adalah alat bantu untuk mempermudah usaha. Pekerjaan mengangkat atau memindahkan beban-beban berat akan menjadi ringan dengan bantuan pesawat sederhana.
Tuas atau pengungkit merupakan satu di antara sekian jenis pesawat sederhana tersebut. Seperti apa cara kerja dari alat ini?
Nah, kalian akan mengetahuinya lewat materi ini. Kakak akan menjelaskan semua hal yang berkaitan dengan tuas (pengungkit), simak dengan baik yah...
Pengertian Tuas (Pengungkit)
Apa yang dimaksud dengan tuas? Tuas disebut juga dengan pengungkit. Dalam ilmu fisika, tuas (pengungkit) adalah pesawat sederhana yang terdiri dari sebuah batangan kokoh yang dapat berputar mengelilingi sebuah titik.
Berikut ini gambar skema sederhana sebuah tuas atau pengungkit:

Tuas (pengungkit) adalah suatu alat yang dapat digunakan untuk mempermudah melakukan usaha. Alat ini sering difungsikan sebagai alat bantu untuk mengangkat, memindahkan, atau mencongkel barang/benda.
Dengan tuas (pengungkit), maka proses pemindahan barang membutuhkan energi yang lebih sedikit dibandingkan tanpa tuas (pengungkit).
Tuas adalah suatu alat yang memudahkan manusia dalam melakukan usaha/kerja tanpa mengurangi berat benda. Tuas atau pengungkit dapat memudahkan usaha dengan cara menggandakan gaya kuasa dan mengubah arah gaya.
Berikut ini adalah contoh gambar penggunaan tuas (pengungkit) untuk mengangkat/memindahkan beban:

Bagian-Bagian Tuas (Pengungkit)
Tuas (pengungkit) mempunyai tiga bagian utama, yaitu titik kuasa, titik tumpu, dan titik beban. Berikut ini penjelasan dari masing-masing bagian tersebut:
1. Titik Kuasa Tuas (Pengungkit)
Titik kuasa adalah bagian dari pengungkit yang diberi tenaga (gaya) agar benda terangkat. Gaya yang diberikan pada titik tersebut dinamakan gaya kuasa. Sementara itu, jarak dari titik kuasa ke titik tumpu disebut lengan kuasa.
 Contoh alat yang tergolong tuas jenis pertama adalah tang, papan jungkat jungkat, neraca sama lengan, dan gunting.
Contoh alat yang tergolong tuas jenis pertama adalah tang, papan jungkat jungkat, neraca sama lengan, dan gunting.
 Contoh alat dalam kehidupan sehari-hari yang tergolong tuas jenis pertama adalah gerobak dorong roda satu, alat pemecah biji, dan alat pembuka tutup botol.
Contoh alat dalam kehidupan sehari-hari yang tergolong tuas jenis pertama adalah gerobak dorong roda satu, alat pemecah biji, dan alat pembuka tutup botol.
 Contoh alat dalam kehidupan sehari-hari yang tergolong tuas jenis ketiga adalah sekop dan pinset.
Contoh alat dalam kehidupan sehari-hari yang tergolong tuas jenis ketiga adalah sekop dan pinset.
Keterangan:
Keterangan:
l = 1,5 m
w = 1.200 N
lb = 0,5 m
lk = l - lb
= 1,5 - 0,5
= 1 m
Ditanyakan:
F....?
Penyelesaian:
F = lb/lk . w
= 0,5/1 . 1.200
= 600 N
Jadi, gaya yang harus dikeluarkan untuk mengangkat batu tersebut adalah 600 N.
A. Gaya yang Diperlukan
B. KM
w = 900 N
l = 2 m
lb = 50 cm = 0,5 m
lk = l - lb
= 2 - 0,5
= 1,5 m
Ditanyakan:
A. F...?
B. KM...?
Penyelesaian:
A. Gaya yang diperlukan (F)
F = lb/lk . w
= 0,5/1,5 . 900
= 300 N
Jadi, gaya yang harus dikeluarkan untuk mengangkat batu tersebut adalah 300 N
2. Titik Tumpu
Titik tumpu (fulcrum) adalah titik di mana tuas (pengungkit) bertumpu (berpusat). Hakikatnya, titik ini adalah sebuah penyokong, atau kaki, yang ditempatkan sedemikian rupa sehingga memungkinkan sejumlah tekanan yang relatif kecil untuk mengangkat beban yang bobotnya relatif berat.3. Titik Beban
Titik beban adalah titik tempat beban (beban atau barang yang akan dijungkit) bertumpu. Beban adalah gaya yang akan dikalahkan. Sementara itu, jarak dari titik beban ke titik tumpu disebut lengan beban.Prinsip Kerja Tuas (Pengungkit)
Prinsip kerja tuas (pengungkit) adalah memperbesar gaya angkat dengan cara memperpanjang lengan kuasa. Besar gaya yang diperlukan untuk mengangkat beban bergantung pada perbandingan panjang lengan kuasa dan lengan beban:- Jika panjang lengan kuasa lebih panjang daripada lengan beban, maka untuk mengangkat benda diperlukan gaya yang lebih kecil.
- Jika panjang lengan kuasa lebih pendek daripada lengan beban, maka untuk mengangkat benda diperlukan gaya yang lebih besar.
Fungsi Tuas (Pengungkit)
Tuas (pengungkit) adalah pesawat sederhana dengan fungsi utama:- mempermudah usaha atau kerja
- memudahkan dalam menggerakkan atau mengangkat beban
- alat pembesar gaya, gaya yang dihasilkan lebih besar daripada gaya yang dikeluarkan.
Jenis-Jenis Tuas (Pengungkit)
Tuas (pengungkit) dibedakan menjadi tiga jenis/golongan, yaitu: tuas jenis pertama, jenis kedua, dan jenis ketiga.1. Tuas (Pengungkit) Jenis/Golongan Pertama
Tuas (pengungkit) jenis golongan kedua merupakan tuas dengan titik tumpu terletak antara titik beban dan titik kuasa atau titik tumpu terletak di antara dua beban.
2. Tuas (Pengungkit) Jenis/Golongan Kedua
Tuas (pengungkit) jenis golongan kedua merupakan tuas dengan titik beban terletak antara titik tumpu dan titik kuasa.
3. Tuas (Pengungkit) Jenis/Golongan ketiga
Tuas (pengungkit) jenis golongan kedua merupakan tuas dengan titik kuasa terletak antara titik tumpu dan titik beban.
Rumus Tuas (Pengungkit)
Rumus pada tuas (pengungkit) jenis pertama, kedua, dan ketiga adalah sebagai berikut:
w . lb = F . lk
atau
w/F = lk/lb
di mana, w = m . gKeterangan:
- w = berat benda (N)
- lb = lengan beban (m)
- F = gaya kuasa (N)
- lk = lengan kuasa (m)
- m = massa benda (kg)
- g = percepatan gravitasi (m/s2)
Rumus Mencari Gaya Pada Tuas (Pengungkit)
F = lb/lk . w
Rumus Mencari Berat Beban Pada Tuas (Pengungkit)
w = lk/lb . F
Rumus Mencari Lengan Kuasa Pada Tuas (Pengungkit)
lk = w/F . lb
Rumus Mencari Lengan Beban Pada Tuas (Pengungkit)
lb = F/w . lk
Keuntungan Mekanis (Mekanik) Tuas/Pengungkit
Keuntungan mekanis tuas (pengungkit) adalah perbandingan antara besar beban dan besar gaya yang dikeluarkan untuk mengimbangi beban atau perbandingan antara lengan kuasa dan lengan beban.Rumus Keuntungan Mekanis Tuas (Pengungkit)
Berdasarkan definisi di atas, maka rumus keuntungan mekanis (mekanik) tuas atau pengungkit adalah:
KM = w/F atau KM = lk/lb
Keterangan:
- KM = Keuntungan mekanis (mekanik)
Contoh Tuas (Pengungkit) dalam Kehidupan Sehari-hari
Berikut ini adalah beberapa 10 contoh alat dalam kehidupan sehari-hari yang menggunakan prinsip kerja tuas (pengungkit):- Tang
- Neraca sama lengan
- Jungkat jungkit
- Palu Pencabut Paku
- Gunting
- Gerobak dorong satu roda
- Pemecah biji
- Pembuka tutup botol
- Sekop
- Pinset
Contoh Soal Tuas (Pengungkit)
Berikut ini adalah beberapa contoh soal tentang tuas (pengungkit):Contoh Soal 1
Tuas dengan titik tumpu berada di antara titik beban dan titik kuasa disebut?Jawaban:
Tuas jenis/golongan pertama.Contoh Soal 2
Tuas yang panjangnya 1,5 m digunakan untuk mengangkat batu seberat 1.200 N. Jika titik tumpu diletakkan 0,5 m dari batu, hitung besar gaya yang harus dikeluarkanJawaban:
Diketahui:l = 1,5 m
w = 1.200 N
lb = 0,5 m
lk = l - lb
= 1,5 - 0,5
= 1 m
Ditanyakan:
F....?
Penyelesaian:
F = lb/lk . w
= 0,5/1 . 1.200
= 600 N
Jadi, gaya yang harus dikeluarkan untuk mengangkat batu tersebut adalah 600 N.
Contoh Soal 3
Sebuah batu yang beratnya 900 N diangkat dengan tuas yang panjangnya 2 m. Jika lengan beban 50 cm dan titik tumpu berada di antara beban dan kuasa. Hitunglah!A. Gaya yang Diperlukan
B. KM
Jawaban:
Diketahui:w = 900 N
l = 2 m
lb = 50 cm = 0,5 m
lk = l - lb
= 2 - 0,5
= 1,5 m
Ditanyakan:
A. F...?
B. KM...?
Penyelesaian:
A. Gaya yang diperlukan (F)
F = lb/lk . w
= 0,5/1,5 . 900
= 300 N
Jadi, gaya yang harus dikeluarkan untuk mengangkat batu tersebut adalah 300 N
B. Keuntungan Mekanis (KM)
KM = w/F
= 900/300
= 3
Jadi, keuntungan mekanis (KM) tuas tersebut adalah 3.
Contoh Soal 4
Tuas dalam keadaan seimbang saat posisi beban dan kuasa seperti gambar: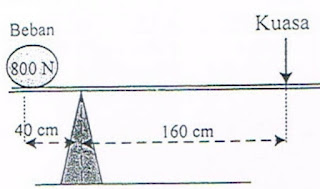
Jika titik tumpu kemudian digeser 10 cm mendekati beban, agar tuas tetap seimbang yang harus dilakukan adalah…
A. Mengurangi kuasa sebesar 10 N
B. Menambah kuasa agar menjadi 200 N
C. Menggeser kuasa mendekati titik tumpu sejauh 50 cm
D. Menggeser kuasa mendekati titik tumpu sejauh 40 cm
Jawaban: C. Menggeser kuasa mendekati titik tumpu sejauh 50 cm
Pembuktian:
Diketahui:- w = 800 N
- lb = 40 cm = 0,4 m
- lk = 160 cm = 1,6 m
- Apa yang harus dilakukan agar tuas tetap seimbang jika titik tumpu digeser 10 cm mendekati beban?
Syarat agar terjadi kesetimbangan pada tuas adalah jika bagian beban sama dengan bagian kuasa:
w . lb = F . lk
Langkah pertama, kita cari terlebih dahulu besar gaya kuasa (F) pada gambar:
F = lb/lk . w
= 0,4/1,6 . 800
= 200 N
Jadi, besar gaya kuasa pada gambar adalah 200 N.
Langkah kedua, menggeser titik tumpu 10 cm atau 0,1 m ke titik beban. Setelah digeser, maka kondisi yang terjadi:
- lengan beban berkurang 0,1 m
- lengan kuasa bertambah 0,1 m
800 . (0,4 - 0,1) = 200 . (1,6 + 0,1)
800 . 0,3 = 200 . 1,7
240 = 340 (Belum seimbang)
Untuk membuatnya seimbang, maka kita geser kuasa mendekati titik tumpu sejauh 50 cm atau 0,5 m, artinya panjang lengan kuasa akan berkurang 0,5 m.
w . lb = F . (lk - 0,5)
800 . 0,3 = 200 . (1,7 - 0,5)
240 = 20 . 1,2
240 = 240 (Seimbang)
Jadi, terbukti bahwa tuas menjadi seimbang dengan menggeser kuasa mendekati titik tumpu sejauh 50 cm (Pilihan C).

C. 1, tumpu T di titik 5 dan F di titik 6
D. 3, tumpu T di titik 4 dan F di titik 7
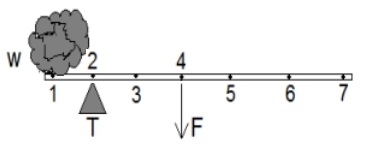
A. 1, tumpu T di titik 2 dan F di titik 4, pada kondisi ini lk = 2 dan lb = 1, artinya gaya kuasa agak kecil. Berikut ini gambarnya:
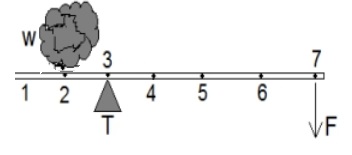
B. 2, tumpu T di titik 3 dan F di titik 7, pada kondisi ini lk = 4 dan lb = 1, artinya gaya kuasa paling kecil. Berikut ini gambarnya:
 C. 1, tumpu T di titik 5 dan F di titik 6, pada kondisi ini lk = 1 dan lb = 4, artinya gaya kuasa paling besar. Berikut ini gambarnya:
C. 1, tumpu T di titik 5 dan F di titik 6, pada kondisi ini lk = 1 dan lb = 4, artinya gaya kuasa paling besar. Berikut ini gambarnya:
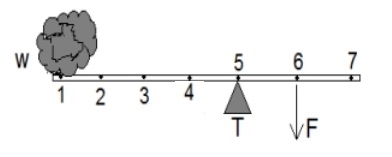 D. 3, tumpu T di titik 4 dan F di titik 7, pada kondisi ini lk = 3 dan lb = 1, artinya gaya kuasa kecil. Berikut ini gambarnya:
D. 3, tumpu T di titik 4 dan F di titik 7, pada kondisi ini lk = 3 dan lb = 1, artinya gaya kuasa kecil. Berikut ini gambarnya:
Gimana adik-adik, udah paham kan materi tuas (pengungkit) di atas? Jangan bingung lagi yah.
Sekian dulu materi kali ini, bagikan agar teman yang lain bisa membacanya. Terima kasih, semoga bermanfaat.
240 = 340 (Belum seimbang)
Untuk membuatnya seimbang, maka kita geser kuasa mendekati titik tumpu sejauh 50 cm atau 0,5 m, artinya panjang lengan kuasa akan berkurang 0,5 m.
w . lb = F . (lk - 0,5)
800 . 0,3 = 200 . (1,7 - 0,5)
240 = 20 . 1,2
240 = 240 (Seimbang)
Jadi, terbukti bahwa tuas menjadi seimbang dengan menggeser kuasa mendekati titik tumpu sejauh 50 cm (Pilihan C).
Contoh Soal 5
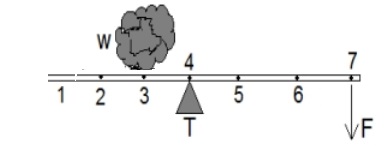
Perhatikan gambar berikut!
Tuas ini akan gaya menghasilkan kuasa F paling kecil bila beban w di letakkan titik...
A. 1, tumpu T di titik 2 dan F di titik 4
B. 2, tumpu T di titik 3 dan F di titik 7C. 1, tumpu T di titik 5 dan F di titik 6
D. 3, tumpu T di titik 4 dan F di titik 7
Jawaban: B. 2, tumpu T di titik 3 dan F di titik 7
Pembuktian:
Maksud dari soal ini adalah hanya dengan gaya kuasa kecil beban bisa terangkat.
Besar gaya angkat pada tuas dipengaruhi oleh panjang lengan kuasa dan panjang lengan beban:
- Jika lengan kuasa lebih panjang dari lengan beban, maka gaya kuasa kecil.
- Jika lengan kuasa lebih pendek dari lengan beban, maka gaya kuasa besar.
A. 1, tumpu T di titik 2 dan F di titik 4, pada kondisi ini lk = 2 dan lb = 1, artinya gaya kuasa agak kecil. Berikut ini gambarnya:

B. 2, tumpu T di titik 3 dan F di titik 7, pada kondisi ini lk = 4 dan lb = 1, artinya gaya kuasa paling kecil. Berikut ini gambarnya:



Kesimpulan
Tuas (pengungkit) adalah pesawat sederhana yang terdiri dari sebuah batangan kokoh yang dapat berputar mengelilingi sebuah titik.Gimana adik-adik, udah paham kan materi tuas (pengungkit) di atas? Jangan bingung lagi yah.
Sekian dulu materi kali ini, bagikan agar teman yang lain bisa membacanya. Terima kasih, semoga bermanfaat.
