Rumus Percepatan dan Cara Menggunakannya (Contoh Soal)

Daftar Isi

Halo adik-adik, kali ini kakak akan menjelaskan satu rumus penting dalam gerak, yaitu rumus percepatan beserta cara menggunakannya ke dalam soal. Mengapa penting? Sebab, rumus ini kerap digunakan setiap kita melakukan perhitungan tentang gerak benda.

Secara spesifik, materi percepatan akan kita temui dalam materi bab gerak benda, khususnya gerak lurus berubah beraturan (GLBB). Ketika membaca materi ini, kakak anggap materi fisika kalian di sekolah telah sampai di bab tersebut.

Namun, kalian tenang aja, rumus ini tidak sulit kok. Kakak yakin setelah mempelajari materi ini, kalian pasti bisa menerapkannya ke dalam soal.

Baiklah, kakak mulai saja materinya...

Pengertian Percepatan

Apa sih percepatan itu? Disadari atau tidak, sebenarnya dalam kehidupan sehari-hari kita sangat akrab dengan percepatan. Misalnya, ketika kalian berjalan, ada kalanya berjalan pelan, tetapi pada saat tertentu berjalan cepat. Perubahan berjalan dari pelan ke cepat itu menandakan bahwa kalian sedang melakukan percepatan.

Begitupun pada saat kalian berkendara, ada kalanya kendaraan yang kalian tumpangi melaju pelan, namun pada saat tertentu melaju cepat. Artinya, kendaraan yang kalian tumpangi juga sedang melakukan percepatan.

Gimana adik-adik? Dari ilustrasi di atas, udah dapat gambaran mengenai apa itu percepatan? Yah benar, jadi:

Percepatan (acceleration) adalah perubahan kecepatan dalam selang waktu tertentu¹

Berdasarkan definisi di atas, maka benda yang mengalami perubahan kecepatan berarti sedang melakukan percepatan. Perubahan kecepatan itu bisa bertambah cepat atau bertambah lambat. Jika bertambah cepat artinya percepatannya positif, namun jika bertambah lambat artinya percepatannya negatif. Percepatan negatif disebut juga dengan perlambatan.

Percepatan positif adalah percepatan yang searah dengan gerak benda. Sedangkan, percepatan negatif adalah percepatan yang berlawanan arah dengan benda.

Beberapa contoh percepatan positif dalam kehidupan sehari-hari:

• Gerak buah mangga yang jatuh dari pohonnya akan semakin cepat sebelum menyentuh tanah.
• Gerak sepeda motor yang melaju pada jalan menurun.
• Gerak mobil yang akan bertambah cepat ketika pedal gas diinjak.

Berikut ini adalah beberapa contoh percepatan negatif (perlambatan) dalam kehidupan sehari-hari:

• Gerak bola yang dilempar ke atas, maka gerakannya akan bertambah lambat sebelum mencapai puncak.
• Gerak mobil yang melaju pelan sampai berhenti ketika pedal rem diinjak.
• Gerak sepeda yang dikayuh di jalan menanjak

Dalam fisika, percepatan disimbolkan dengan (a), dengan satuan (^m/_s²). Percepatan merupakan besaran turunan karenan tersusun dari beberapa besaran pokok. Selain itu, percepatan juga termasuk ke dalam besaran vektor sehingga untuk menyatakannya harus dengan angka dan arah.

Rumus Umum Percepatan

Secara umum, rumus percepatan sering ditulis dengan persamaan:

 a = ^{Δ v} / _{Δ t} = ^{v₂ - v₁} / _{t2 - t1}

Keterangan:

• a = percepatan benda (^m/_s²)
• Δv = perubahan kecepatan (^m/_s)
• Δt = selang waktu (s)
• v₂ = kecepatan akhir (^m/_s)
• v₁ = kecepatan awal (^m/_s)
• t₂  = waktu akhir (s)
• t₁  = waktu awal (s)

Coba perhatikan rumus di atas, ada simbol yang dicetak tebal (bold), ada yang tidak. Mengapa begitu? Jadi, simbol yang dicetak tebal menandakan bahwa simbol itu adalah besaran vektor.

Percepatan menghubungkan 2 besaran, yaitu kecepatan dan waktu. Jika dituliskan dalam grafik, maka bentuknya sebagai berikut:

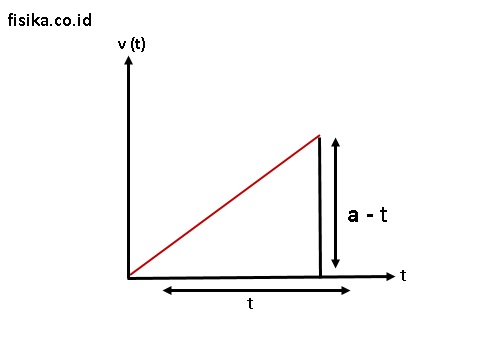
Jenis-Jenis Percepatan

Di dalam gerak lurus, terdapat dua jenis percepatan, yaitu percepatan rata-rata dan percepatan sesaat. Pembagian jenis percepatan ini untuk menghadapi fakta bahwa sangat sulit menemukan sebuah benda dalam kehidupan sehari-hari yang bergerak dengan percepatan tetap (konstan).

Kebanyakan benda bergerak dengan percepatan berubah-ubah, sehingga terdapat kesulitan tersendiri untuk menghitung nilai percepatan secara tepat.

Untuk memudahkan perhitungan, konsep gerak membagi percepatan tersebut menjadi percepatan rata-rata dan percepatan sesaat.

1. Percepatan Rata-rata (Average Acceleration)

Percepatan rata-rata (average acceleration) didefinisikan sebagai perubahan kecepatan dalam selang waktu tertentu. Artinya, dalam selang waktu tertentu percepatan gerak dapat berubah-ubah. Adapun percepatan rata-rata dapat mewakili nilai percepatan selama selang waktu tersebut.

Rumus Percepatan Rata-rata

Secara matematis, percepatan rata-rata dirumuskan dengan persamaan:

 a = ^{Δ v} / _{Δ t} = ^{v₂ - v₁} / _{t2 - t1}

Keterangan:

• a = percepatan rata-rata (^m/_s²)
• Δv = perubahan kecepatan (^m/_s), dibaca "delta v"
• Δt = selang waktu (s), dibaca "delta t"
• v₂ = kecepatan akhir (^m/_s)
• v₁ = kecepatan awal (^m/_s)
• t₂  = waktu akhir (s)
• t₁  = waktu awal (s)

Catatan: Jika di soal hanya disebutkan "percepatan" saja, maka yang dimaksud adalah "percepatan rata-rata".

2. Percepatan Sesaat (Instantaneous Acceleration)

Percepatan sesaat (instantaneous acceleration) adalah percepatan rata-rata dengan selang waktu yang sangat kecil (mendekati nol). 

Dalam bahasa yang lain, percepatan sesaat adalah limit dari percepatan rata-rata pada saat selang waktu mendekati nol. Percepatan sesaat sama dengan laju perubahan sesaat dari kecepatan terhadap waktu.

Rumus Percepatan Sesaat

Berdasarkan definisi di atas, maka rumus percepatan sesaat dituliskan dengan bentuk persamaan: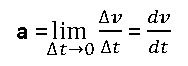

Keterangan:

• a = percepatan sesaat (^m/_s²)
• Δv = perubahan kecepatan (^m/_s)
• Δt = selang waktu (s)

Cara Menggunakan Rumus Percepatan

Sebenarnya, tidak sulit untuk menerapkan rumus percepatan ini ke dalam perhitungan. Kalian hanya perlu memasukkan nilai-nilai sesuai dengan simbol yang tertera pada rumus. Setelah itu, maka operasi perhitungan bisa langsung dilakukan.

Jadi, langkah-langkah yang harus kalian lakukan untuk menggunakan rumus ini adalah sebagai berikut:

1. Identifikasi Besaran Kecepatan

Pada rumus percepatan (a), terdapat simbol perubahan kecepatan (Δv). Ingat, jika terdapat simbol delta (Δ), maka itu artinya terdapat dua besaran yang saling diperkurangkan, dalam hal ini Δv berarti v₂ - v₁. 

Oleh karena itu, ada dua nilai kecepatan yang harus kalian cari, yaitu kecepatan 1 (v₁) dan kecepatan 2 (v₂). Di dalam rumus, nilai kecepatan 2 akan diperkurangkan dengan nilai kecepatan 1.

2. Identifikasi Besaran Waktu

Langkah selanjutnya adalah kalian harus menemukan besaran selang waktu (Δt). Sama dengan penjelasan di atas, ada 2 nilai besaran waktu yang harus kalian cari, yaitu waktu 1 (t₁) dan waktu 2 (t₂).

Di dalam rumus percepatan, nilai waktu 2 (t₂) akan diperkurangkan dengan nilai waktu 1 (t₁).

3. Membagi Kecepatan dengan Selang Waktu

Bentuk rumus percepatan adalah operasi pembagian, di mana nilai dari kecepatan akan dibagi dengan nilai dari selang waktu. Hasil pembagian itulah yang menjadi nilai akhir percepatan (a).

Contoh Soal Percepatan

Nah, sekarang kita akan praktikkan langkah-langkah di atas ke dalam contoh soal percepatan berikut ini:

Contoh Soal 1

Sebuah balok kayu dilepaskan dari keadaan diam pada sebuah bidang miring. Dalam selang waktu 5 sekon, kecepatan balok menjadi 4 m/s. Tentukanlah percepatan rata-rata yang dialami balok.

Jawaban: 

Diketahui:

• v₁ = 0 m/s (keadaan diam)
• t₁ = 0 s
• t₂ = 5 s
• v₂ = 4 m/s

Ditanyakan:

• a.....? 

Penyelesaian:
a = ^{Δ v}/_{Δ t}
   = ^{v₂ - v₁}/_{t2 - t1}
   = ^{₄ - ₀}/_{5 - 0}

   = ^₄/₅ 
   =0,8 ^m/_s²

Contoh Soal 2

Mobil Pak Budi pada detik pertama bergerak dengan kecepatan 5 m/s. Pada detik kedua, kecepatannya menjadi 8 m/s. Berapakah percepatan mobil tersebut?

Jawaban: 

Diketahui:

• v₁ = 5 m/s
• t₁ = 1 s
• t₂ = 2 s
• v₂ = 8 m/s

Ditanyakan:

• a.....? 

Penyelesaian:
a = ^{Δ v}/_{Δ t}
   = ^{₈ - ₅}/_{2 - 1}
   = _³/₁
   = 3 ^m/_s²

Contoh Soal 3

Pak Andi mengendarai sepeda sepanjang lintasan lurus dengan persamaan kecepatan v = (2t + 4) m/s, dengan t dalam sekon. Tentukanlah percepatan rata-rata sepeda dalam selang waktu t₁ = 1 sekon dan t₂ = 3 sekon.

Jawaban: 

Diketahui:

• Untuk t₁ = 1 s, maka v₁ = 2(1) + 4 = 6 m/s
• Untuk t₂ = 3 s, maka v₂ = 2(3) + 4 = 10 m/s

Ditanyakan:

• a.....? 

Penyelesaian:
a = ^{Δ v}/_{Δ t}
   = ^{₁₀ - ₆}/_{3 - 1}
   = _⁴ / ₂
   = 2 ^m/_s²

Contoh Soal 4

Seekor kuda balap berlari dipercepat. Mula-mula diam. Setelah 5 detik kecepatannya menjadi 15 m/s. Hitung berapa percepatan kuda tersebut?

Jawaban: 

Diketahui:

• v₁ = 0 m/s (keadaan diam)
• t₁ = 0 s
• t₂ = 5 s
• v₂ = 15 m/s

Ditanyakan:

• a.....? 

Penyelesaian:
a = ^{Δ v}/_{Δ t}
   = ^{₁₅ - ₀}/_{5 - 0}
   = _¹⁵/₅
   = 3 ^m/_s²

Contoh Soal 5

Seorang pengemudi mobil mengerem mobilnya yang sedang bergerak dengan kecepatan 30 m/s. Kecepatan mobil berkurang menjadi 10 m/s setelah 5 s. Berapakah percepatan rata-ratanya?

Jawaban: 

Diketahui:

• v₁ = 30 m/s
• t₁ = 0 s
• t₂ = 5 s
• v₂ = 10 m/s

Ditanyakan:

• a.....? 

Penyelesaian:
a = ^{Δ v}/_{Δ t}
   = ^{₁₀ - ₃₀}/_{5 - 0}
   = _{^{- 20}}/₅
   = - 4 ^m/_s²

Contoh Soal 6

Seorang pengendara mobil membawa mobilnya dengan kecepatan 10 m/s. Kemudian, ia menginjak pedal gas selama 4 s sehingga mobil meningkat kecepatannya menjadi 18 m/s. Hitunglah:

a. Percepatan mobil ketika kelajuan mobil bertambah

b. Waktu untuk mempercepat mobil sehingga kelajuannya bertambah dari 18 m/s menjadi 34 m/s dengan percepatan pada soal a.

Jawaban: 

Diketahui:

• v₁ = 10 m/s
• t₁ = 0 s
• t₂ = 4 s
• v₂ = 18 m/s

Ditanyakan:

• a.....? 
• Δt pada v₁ = 18 m/s dan v₂ = 34 m/s

Penyelesaian:
a = ^{Δ v}/_{Δ t}
   = ^{₁₈ - ₁₀}/_{4 - 0}
   = _⁸/₄
   = 2 ^m/_s² (jawaban pertanyaan a)
Δt = ^{Δ v}/_a
    = ^{₃₄ - ₁₈}/₂
    = _¹⁶/₂
    = 8 s (jawaban pertanyaan b)

Contoh Soal 7

Sebuah mobil van mulai bergerak dengan percepatan tetap dan kecepatannya meningkat menjadi 20 m/s dalam waktu 5 s. Sopir mobil van terus mempertahankan laju mobil dengan kecepatan ini selama 10 s. Kemudian, ia mengerem dan menurunkan kecepatannya hingga menjadi 12 m/s dalam waktu 4 s. Tentukanlah:

a. Percepatan rata-rata pada saat 5 s pertama.
b. Percepatan antara t₁ = 5 s hingga t₂ = 15 s
c. Percepatan rata-rata pada saat 4 s terakhir

Jawaban: 

Diketahui:

• v₁ = 10 m/s
• t₁ = 0 s
• t₂ = 4 s
• v₂ = 18 m/s

Ditanyakan:

• a.....? 
• Δt pada v₁ = 18 m/s dan v₂ = 34 m/s

Penyelesaian:
a. Percepatan rata-rata mobil pada 5 s pertama

a = ^{Δ v}/_{Δ t}
   = ^{₂₀ - ₀}/_{5 - 0}
   = _²⁰/₅
   = 4 ^m/_s²

b. Mobil van bergerak dengan kecepatan tetap antara t = 5 s dan t = 15 s. Percepatan dalam selang waktu ini adalah nol karena tidak ada perubahan kecepatan. 

c. Percepatan rata-rata pada 4 s terakhir

a = ^{Δ v}/_{Δ t}
   = ^{₁₂ - ₂₀}/_{19 - 15}
   = _^-8/₄
   = - 2 ^m/_s²

Contoh Soal 8

Sebuah motor mula-mula bergerak lurus dengan laju 15 m/s. Pengemudinya kemudian memutar panel gas sehingga motor mendapat percepatan sebesar 1,2 ^m/_s². Hitunglah kecepatan motor setelah 5 sekon.

Jawaban: 

Diketahui:

• v₁ = 15 m/s
• a = 1,2 ^m/_s²
• t₂ = 5 s
• t₁ = 0 s

Ditanyakan:

• v₂.....? 

Penyelesaian:
a = ^{Δ v}/_{Δ t}
v₂ - v₁ = a x Δt
v₂  = v₁ + a x Δt
     = 15 + (1,2 (5-0))
     = 15 + 6
     = 21 m/s

Contoh Soal 9

Sebuah motor dipercepat dari keadaan diam dengan percepatan tetap sebesar 6 ^m/_s². Hitunglah waktu yang dibutuhkan motor agar bisa mencapai kelajuan 48 m/s. 

Jawaban: 

Diketahui:

• a = 6 ^m/_s²
• v₁ = 0 ^m/_s
• v₂ = 48 ^m/_s
• t₁ = 0 s

Ditanyakan:

• t₂.....? 

Penyelesaian:
a = ^{Δ v}/_{Δ t}
t₂ - t₁ = ^{Δ v}/_a 
t₂  = t₁ + ^{Δ v}/_a
    = 0 + ^{₄₈ - ₀}/₆
    = 0 + 8
    = 8 s

Contoh Soal 10

Sebuah mobil melaju dengan kecepatan 30 m/s. Lalu mobil itu direm hingga berhenti dalam waktu 10 sekon. Hitunglah percepatan mobil tersebut?

Jawaban: 

Diketahui:

• v₁ = 30 ^m/_s
• v₂ = 0 ^m/_s
• t₁ = 0 s
• t₂ = 10 s

Ditanyakan:

• a.....? 

Penyelesaian:
a = ^{Δ v}/_{Δ t}
   = ^{₀ - ₃₀}/_{10 - 0}
   = _^-30/₁₀
   = - 3 ^m/_s²

Contoh Soal 11

Sebuah sepeda motor memiliki kecepatan 20 m/s. Berapa kecepatan akhir motor jika mengalami percepatan 4 ^m/_s² selama 5 sekon? 

Jawaban: 

Diketahui:

• v₁ = 20 ^m/_s
• t₁ = 0 s
• t₂ = 5 s 
• a = 4 ^m/_s²

Ditanyakan:

• v₂.....? 

Penyelesaian:
a = ^{Δ v}/_{Δ t}
v₂ - v₁ = a x Δt
v₂  = v₁ + a x Δt
     = 20 + (4 (5-0))
     = 20 + 20
     = 40 m/s

Contoh Soal 12

Pak Gunawan mengendarai motor sepanjang lintasan lurus dengan persamaan kecepatan v = (2t + 4) m/s, dengan t dalam sekon. Tentukanlah percepatan rata-rata motor dalam selang waktu t₁ = 1 sekon dan t₂ = 3 sekon.

Jawaban: 

Diketahui:

• Untuk t₁ = 1 s, maka v₁ = 2(1) + 4 = 6 m/s
• Untuk t₂ = 3 s, maka v₂ = 2(3) + 4 = 10 m/s

Ditanyakan:

• a.....? 

Penyelesaian:
a = ^{Δ v}/_{Δ t}
   = ^{₁₀ - ₆}/_{3 - 1}
   = _⁴ / ₂
   = 2 ^m/_s²

Gimana adik-adik, udah paham kan materi rumus percepatan di atas? Kalian juga pasti bisa kok menggunakannya.

Sekian dulu materi kali ini, bagikan agar teman yang lain bisa membacanya. Terima kasih, semoga bermanfaat.

Referensi:

• Yaz, M. Ali. 2007. Fisika 1 SMA Kelas X. Jakarta: Yudhistira
• Young, Hugh D. 2002. Fisika Universitas. Jakarta: Erlangga.